Syslab使用手册
⋮

# curl

向量场的旋度和角速度

函数库: TyPlot

# 语法

curlx,curly,curlz,cav = curl(X,Y,Z,Fx,Fy,Fz;nargout=4)

curlx,curly,curlz,cav = curl(Fx,Fy,Fz;nargout=4)

curlz,cav = curl(X,Y,Fx,Fy;nargout=2)

curlz,cav = curl(Fx,Fy;nargout=2)

cav = curl(___)

# 说明

curlx, curly, curlz, cav = curl (X, Y, Z, Fx, Fy, Fz; nargout=4) 计算具有向量分量 Fx、Fy 和 Fz 的三维向量场的数值旋度和角速度。输出 curlx、curly 和 curlz 表示旋度的向量分量，cav 表示旋度的角速度。

数组 X、Y 和 Z 用于定义向量分量 Fx、Fy 和 Fz 的坐标，它们必须是单调的，但间距无需一致。X、Y 和 Z 必须为大小相同的三维数组，可以由 meshgrid3 生成。示例

curlx, curly, curlz, cav = curl(Fx, Fy, Fz; nargout=4) 假定一个默认的样本点网格。默认网格点 X、Y 和 Z 由表达式 X, Y, Z = meshgrid3(1:n, 1:m, 1:p) 确定，其中 m, n, p = size(Fx)。如果您希望节省内存且不在意样本点之间的绝对距离，则可使用此语法。

curlz, cav = curl (X, Y, Fx, Fy; nargout=2) 计算具有向量分量 Fx 和 Fy 的二维向量场的数值旋度和角速度。输出 curlz 表示旋度的 z 分量，cav 表示旋度的角速度。

矩阵 X 和 Y 用于定义 Fx 和 Fy 坐标，它们必须是单调的，但间距无需一致。X 和 Y 必须为大小相同的二维矩阵，可以由 meshgrid2 生成。示例

curlz, cav = curl (Fx, Fy; nargout=2) 假定一个默认的样本点网格。默认网格点 X 和 Y 由表达式 X,Y = meshgrid2(1:n, 1:m) 确定，其中 m, n = size(Fx)。如果您希望节省内存且不在意样本点之间的绝对距离，则可使用此语法。

cav = curl(___) 仅返回向量场的角速度。示例

# 示例

在一个平面上显示旋度和角速度

加载一个表示风场的三维向量场数据集。该数据集包含大小为 35×41×15 的数组。

using TyPlot
pkg_dir = pkgdir(TyPlot)
source_path = pkg_dir * "/examples/数据文件/wind.jl"
include(source_path);

计算向量场的数值旋度和角速度。

curlx, curly, curlz, cav = curl(x, y, z, u, v, w; nargout=4);

显示计算得出的旋度和角速度的二维切片。在 z[:, :, 1] 处对数据进行切片，其中 z 坐标等于 -0.002。

k = 1;
xs = x[:, :, k];
ys = y[:, :, k];
zs = z[:, :, k];
us = u[:, :, k];
vs = v[:, :, k];

使用 pcolor 在二维坐标中绘制角速度。使用 quiver 显示向量场的 x 和 y 分量。

s = pcolor(xs, ys, cav[:, :, k])
colorbar(s)
hold("on")
quiver(xs, ys, us, vs, "k")
hold("off")
xlim([70, 134.3])
ylim([17.5, 60])
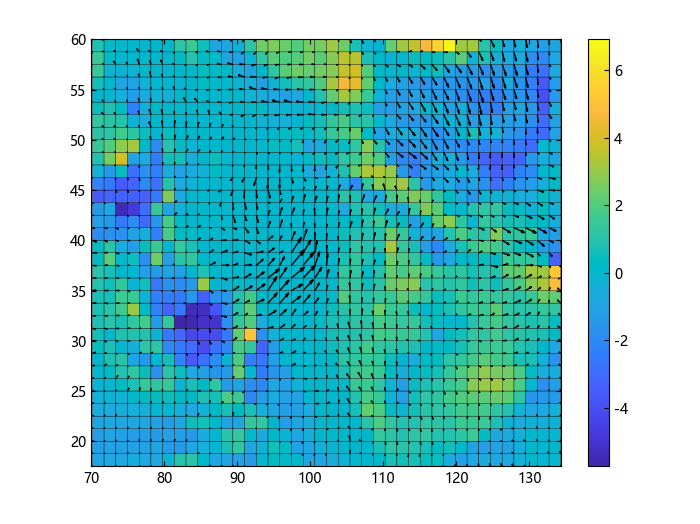
二维向量场的旋度

指定二维坐标和向量场。

using TyPlot
using TyBase
x, y = meshgrid2(-4:4, -4:4)
Fx = -y * 2;
Fy = x * 2;

绘制向量场分量 Fx 和 Fy。

quiver(x,y,Fx,Fy)

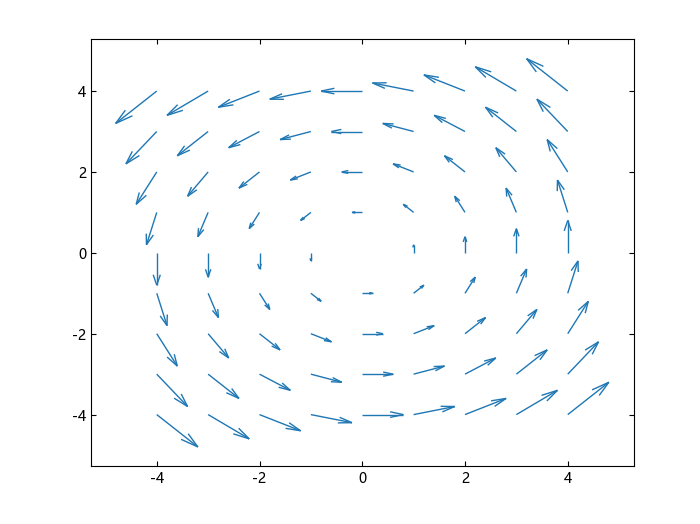
求二维向量场的数值旋度和角速度。旋度和角速度的值在所有输入坐标下均为常量。

curlz, cav = curl(x, y, Fx, Fy; nargout=2)

curlz =
9×9 Matrix{Float64}:
 4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0
 4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0
 4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0
 4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0
 4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0
 4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0
 4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0
 4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0
 4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0  4.0

cav =
9×9 Matrix{Float64}:
 2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0
 2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0
 2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0
 2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0
 2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0
 2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0
 2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0
 2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0
 2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0
计算向量场的角速度

加载一个表示风场的三维向量场数据集。该数据集包含大小为 35×41×15 的数组。

using TyPlot
pkg_dir = pkgdir(TyPlot)
source_path = pkg_dir * "/examples/数据文件/wind.jl"
include(source_path)

计算向量场的角速度。

cav = curl(x, y, z, u, v, w)

35×41×15 Array{Float64, 3}:
[:, :, 1] =
 -0.901955   -0.801247     -0.801247     -0.49424      …   0.000218598  -0.073134   -0.185707   -0.657596
 -1.13808    -1.02055      -1.0206       -0.992699         0.130901     -0.0180788   0.0113751  -0.173855
 -1.13802    -0.906665     -1.07722      -1.25343          0.0727111    -0.13554    -0.121009   -0.138597
 -0.908082   -0.73732      -0.820747     -0.820717        -0.218612     -0.426098   -0.24025    -0.171319
  ⋮                                                    ⋱                                         ⋮
  1.50047    -0.214495     -0.240182     -0.186651        -2.43796      -2.78627    -0.701421   -0.382952
  1.48915     0.256742     -0.000128036  -0.000247954     -1.82454      -2.01532    -0.778741   -0.572104
  0.81442     0.21152      -6.23176e-5   -0.000376832     -0.826521     -1.23089    -0.883022   -0.940157
  0.0680408  -0.000169136  -0.000180922  -0.038525        -8.55551e-6   -0.558658   -0.476864   -0.534427

[:, :, 2] =
 -0.1226    -0.199058   -0.200704   -0.105126  -0.0610882  …   0.283327    0.0566824  -0.27173     -0.560583
 -0.351052  -0.433397   -0.425231   -0.509127  -0.424654       0.115409    0.0509464  -0.0578819   -0.337867
 -0.333022  -0.417986   -0.527721   -0.491273  -0.580938      -0.0320984   0.0904178  -0.00236656  -0.13841
 -0.531616  -0.587766   -0.652502   -0.654452  -0.582751      -0.407718   -0.18516    -0.125821    -0.0789054
  ⋮                                                        ⋱                                        ⋮
  0.169148   0.0362238  -0.0366846  -0.339965  -0.0385081     -1.18205    -1.36279    -0.629501    -0.916605
  0.255707   0.276645    0.267679    0.361245   0.287402      -1.08505    -1.3162     -0.774921    -1.28448
  0.936322   0.366281    0.567779    1.04784    0.753477      -0.994325   -1.27109    -1.0191      -1.32032
  0.695196   0.719228    0.50223     0.870258   1.16786       -0.601821   -1.06296    -1.20316     -1.52127

;;; …

[:, :, 14] =
 -0.0561356  -0.0526157   -0.153529   -0.0375489   …   0.103815  -2.48102   -2.78375   -2.3754    -1.7338
 -0.125123   -0.170463    -0.0190217  -0.12458         0.567654  -2.33802   -2.7863    -2.24907   -1.51715
 -0.230427   -0.0958802   -0.215444   -0.143038        0.907906  -1.96332   -2.46404   -1.88842   -1.18915
 -0.32095    -0.0942211   -0.194823   -0.19387         0.430885  -1.03693   -1.73343   -1.35157   -1.03291
  ⋮                                                ⋱                                               ⋮
 -0.134011   -0.108379    -0.045493    0.0203978       0.445492   0.559381   0.641623   0.692359   0.466367
 -0.229947   -0.189494    -0.0228618  -0.0325694       0.508257   0.596919   0.584161   0.472894   0.292905
 -0.257444   -0.152325    -0.0602232  -0.0622876       0.582155   0.534737   0.438853   0.348916   0.268685
 -0.384616   -0.157511    -0.0427215  -0.0947593       0.524024   0.530448   0.371951   0.369912   0.255158

[:, :, 15] =
 -0.11572   -0.0563277  -0.196715   -0.12685      0.0739448  …  0.175733  -3.04303   -3.35884   -2.96246   -2.45475      
 -0.180145  -0.301774   -0.191878   -0.297415    -0.279105      1.05557   -3.13077   -3.35313   -2.88942   -1.9421       
 -0.32052   -0.0316977  -0.402785   -0.353781    -0.44186       1.70408   -3.06614   -3.03739   -2.5573    -1.75606      
 -0.49979   -0.235458   -0.196499   -0.291787    -0.223292      0.545235  -1.7098    -2.50747   -1.97045   -1.32553          
  ⋮                                                          ⋱                                              ⋮ 
 -0.168721  -0.0413091  -0.077107    0.108554     0.0365782     0.412232   0.592794   0.735141   0.822177   0.929894     
 -0.330913  -0.209066   -0.050654    2.55267e-5  -0.0720212     0.531769   0.657376   0.655137   0.6369     0.747964     
 -0.315258  -0.122162    0.0330301  -0.150461     0.0473115     0.517609   0.52627    0.634261   0.3675     0.19301      
 -0.312366  -0.109146    0.102724   -0.0547611   -0.116916      0.53916    0.472409   0.372427   0.406413   0.164378

# 输入参数

X, Y, Z — 输入坐标
矩阵 | 三维数组

输入坐标，指定为矩阵或三维数组。

  • 对于二维向量场，X 和 Y 必须为相同大小的二维矩阵，并且该大小不能小于 2×2。

  • 对于三维向量场，X、Y 和 Z 必须为相同大小的三维数组，并且该大小不能小于 2×2×2。

数据类型：Float32 | Float64

复数支持：是

Fx, Fy, Fz — 输入坐标中的向量场分量
矩阵 | 三维数组

输入坐标中的向量场分量，指定为矩阵或三维数组。Fx、Fy 和 Fz 的大小必须与 X、Y 和 Z 的大小相同。

数据类型：Float32 | Float64

复数支持：是

# 输出参数

curlx, curly, curlz — 旋度的向量分量
矩阵 | 三维数组

输入坐标中旋度的向量分量，以矩阵或三维数组形式返回。

cav — 角速度
矩阵 | 三维数组

输入坐标中的角速度，以矩阵或三维数组形式返回。

# 详细信息

数值旋度和角速度

向量场的数值旋度是根据向量场在某些点的已知值来估计旋度分量的一种方式。

对于具有三个变量的三维向量场

的旋度定义为

角速度定义为 。

对于具有两个变量的二维向量场

旋度为

角速度定义为 。

# 算法

curl 使用有限差分计算其定义中的偏导数。对于内部数据点，使用中心差分计算偏导数。对于沿边缘的数据点，使用单侧（正向）差分计算偏导数。

例如，假设有一个二维向量场，它由位于 X 和 Y 位置的矩阵 和 表示，大小为 m×n。位置是由 X, Y = meshgrid2(x, y) 创建的二维网格，其中 x 是长度为 n 的向量，y 是长度为 m 的向量。然后 curl 计算偏导数 和 ，如下所示：

  • 内部数据点：

dFy_dx(:, i) = ( Fy(:, i+1) - Fy(:, i-1)) / (x(i+1) - x(i-1)) 和

dFx_dy(j, :) = (Fx(j+1, :) - Fx(j-1, :)) / (y(j+1) - y(j-1))

  • 左边缘和右边缘的数据点：

dFy_dx(:, 1) = (Fy(:, 2) - Fy(:, 1)) / (x(2) - x(1)) 和

dFy_dx(:,n) = (Fy(:,n) - Fy(:,n-1)) / (x(n) - x(n-1))

  • 上边缘和下边缘的数据点：

dFx_dy(1, :) = (Fx(2, :) - Fx(1, :)) / (y(2) - y(1)) 和

dFx_dy(m, :) = (Fx(m, :) - Fx(m-1, :)) / (y(m) - y(m-1))

向量场的数值旋度等于 curlz = dFy_dx - dFx_dy，角速度为 cav = 0.5*curlz。

# 另请参阅

divergence | gradient