# dsp_TransferFunctionEstimator
估计传递函数
函数库: TyDSPSystem
# 说明
dsp_TransferFunctionEstimator 系统对象使用韦尔奇的平均周期图方法计算系统的传递函数。
实现传递函数估计对象:
创建 dsp_TransferFunctionEstimator 对象并设置其属性;
用 step 调用该对象。
# 构造
# 语法
tfe = dsp_TransferFunctionEstimator()
tfe = dsp_TransferFunctionEstimator(; Name = Value)
# 说明
tfe = dsp_TransferFunctionEstimator() 返回一个传递函数估计器对象,它计算实数或复数信号的传递函数。该系统对象使用周期图方法和韦尔奇的平均、修正周期图方法。
tfe = dsp_TransferFunctionEstimator(; Name = Value) 返回一个转移函数估计器对象,每个指定的属性都被设置为指定值。未指定的属性有默认值。
# 属性
除非另有说明,属性是不可调整的,这意味着你在调用对象后不能改变其值。
如果一个属性是可调整的,你可以在任何时候改变它的值。
FFTLengthSource - FFT 长度值的来源"Auto"(默认)| "Property"
FFT 长度值的来源,指定为 "Auto"(默认)或 "Property"。如果你将此属性设置为 "Auto",传递函数估计器会将 FFT 长度设置为输入帧大小。如果你把这个属性设置为 "Property",那么你就用 FFTLength 属性指定 FFT 点的数量。
FFTLength - FFT 长度128 (默认) | 正整数
指定传递函数估计器用来计算交叉频谱估计的 FFT 的长度,作为一个正的整数标量。
当您将 FFTLengthSource 属性设置为 "Property" 时,此属性就会适用。
Window - 窗函数"Hann"(默认)| "Rectangular" | "Chebyshev" | "Flat Top" | "Hamming" | "Kaiser"
为传递函数估计器指定一个窗口函数,作为 "Hann"、"Rectangular"、"Chebyshev"、"Flat Top"、"Hamming"、"Kaiser" 中的一个。
SidelobeAttenuation - 窗口的侧叶衰减60 dB(默认)| 正标量
指定窗口的侧叶衰减为实数、正标量,单位为分贝(dB)。
当你将 Window 设置为 "Chebyshev" 或 "Kaiser" 时,此属性适用。
FrequencyRange - 频谱估计的频率范围"twosided"(默认)| "onesided" | "centered"
指定传递函数估计器的频率范围为 "twosided"、"onesided"、"centered" 之一。
如果你把 FrequencyRange 设置为 "onesided",那么传递函数估计器就会计算实输入信号的单侧频谱;
当 FFT 长度 NFFT 为偶数时,频谱估计的长度为(NFFT/2)+1,并在频率范围 [0, SampleRate/2] 内计算,其中 SampleRate 为输入信号的采样率;
当 NFFT 为奇数时,频谱估计的长度为(NFFT + 1)/2,并在频率范围 [0, SampleRate/2] 内计算。
如果你把 FrequencyRange 设置为 "twosided",那么传递函数估计器就会计算复数或实数输入信号的双侧频谱;
传递函数估计的长度等于 FFT 的长度。传递函数估计是在频率范围 [0, SampleRate] 内计算的,其中 SampleRate 是输入信号的采样率。
如果你把 FrequencyRange 设置为 "centered",那么传递函数估计器就会计算复数或实数输入信号的居中两侧频谱。频谱估计的长度等于 FFT 的长度。当 FFT 长度为偶数时,传递函数估计在频率范围(-SampleRate/2, SampleRate/2)内计算,当 FFT 长度为奇数时,在(-SampleRate/2, SampleRate/2)内计算。
AveragingMethod - 平均数方法"Running"(默认)| "Exponential"
将平均方法指定为 "Running" 或 "Exponential"。在运行平均法中,该对象计算由 SpectralAverages 属性定义的指定数量的传递函数估计值的等权平均数。在指数法中,该对象计算由指数衰减的遗忘因子加权的样本的平均值。
SpectralAverages - 频谱平均数的数量8(默认)| 正整数
频谱平均数的数量,指定为正整数。传递函数估计器通过对最后 N 个估计值进行平均来计算当前的功率谱或功率密度谱估计值。N 是在 SpectralAverages 属性中定义的频谱平均数的数量。
当你将 AveragingMethod 设置为 "Running" 时,此属性适用。
ForgettingFactor - 遗忘因子0.9 (默认) | 范围内的标量 (0,1]
将指数加权遗忘因子指定为大于零且小于等于 1 的标量值。
当你将 AveragingMethod 设置为 "Exponential" 时,该属性适用。
# 用法
# 语法
tfeEst, = step(tfe, x, y)
tfeEst, cxy = step(tfe, x, y)
# 说明
tfeEst, = step(tfe, x, y) 使用韦尔奇的平均周期图法计算输入 x 和输出 y 的系统的传递函数估计值 tfeEst。
tfeEst, cxy = step(tfe, x, y) 还计算了系统的幅度平方相干性估计值 cxy。
# 输入参数
x - 第一个输入数据向量 | 矩阵
第一个输入数据,指定为一个向量或一个矩阵。输入 x 和 y 必须有相同的大小和数据类型。
y - 第二个输入数据向量 | 矩阵
第二个输入数据,指定为一个向量或一个矩阵。输入x 和 y 必须有相同的大小和数据类型。
# 输出参数
tfeEst - 传递函数估计向量 | 矩阵
系统的传递函数估计,其中 x 和 y 分别为输入和输出信号。
该估计值 feEst,等于 pxy./pxx,其中 pxy 是 x 和 y 的交叉功率谱密度,pxx 是 x 的功率谱密度。
传递函数估计值的大小和数据类型与输入值相同。
cxy - 相干性估计向量 | 矩阵
系统的幅度平方相干性估计,以向量或矩阵形式返回。
相干性估计值 cxy 等于(abs(pxy).^2)./(pxx.*pyy),其中 pxy 是 x 和 y 的交叉功率谱密度,pxx 是 x 的功率谱密度,pyy 是 y 的功率谱密度。
相干性估计的大小和数据类型与输入相同。
# 对象函数
要使用对象函数,请将系统对象指定为第一个输入参数。
对系统对象通用的操作
| 函数名 | 简介 |
| step | 运行系统对象算法 |
| reset | 重置系统对象的内部状态 |
| release | 释放资源并允许更改系统对象属性值和输入特征 |
# 示例
估计由 64 阶 FIR 滤波器表示的系统的传递函数
using TyDSPSystem
using TyMath
using TySignalProcessing
rng = MT19937ar(1234)
sine = dsp_SineWave(; Frequency=100, SampleRate=1000, SamplesPerFrame=1000)
tfe = dsp_TransferFunctionEstimator(; FrequencyRange="centered")
plotter = dsp_ArrayPlot(;
PlotType="Line",
XOffset=-500,
YLimits=[-120 5],
Title="System Transfer Function",
YLabel="Frequency Response (dB)",
XLabel="Frequency (Hz)",
)
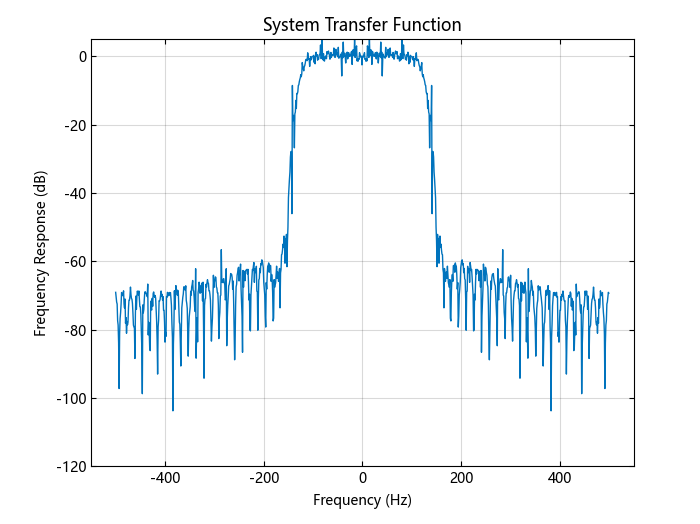
创建一个 64 阶的 FIR 滤波器系统对象,(归一化)截止频率为 1/4。在正弦波中加入随机噪声。逐步通过系统对象以获得数据流,并绘制传递函数的大小对数。
LP = dsp_FIRFilter(; Numerator=fir1(64, 1 / 4))
x = step(sine) + 0.05 * randn(rng, 1000, 1)
y = step(LP, x)
Txy, Cxy = step(tfe, x, y)
step(plotter, 20 * log10.(abs.(Txy)))
# 参考文献
[1] Hayes, Monson H. Statistical Digital Signal Processing and Modeling. Hoboken, NJ: John Wiley & Sons, 1996
[2] Kay, Steven M. Modern Spectral Estimation: Theory and Application. Englewood Cliffs, NJ: Prentice Hall, 1999
[3] Stoica, Petre and Randolph L. Moses. Spectral Analysis of Signals. Englewood Cliffs, NJ: Prentice Hall, 2005
[4] Welch, P. D. ``The use of fast Fourier transforms for the estimation of power spectra: A method based on time averaging over short modified periodograms,'' IEEE Transactions on Audio and Electroacoustics, Vol. 15, pp. 70–73, 1967.